
#Lfsr polynomial how to
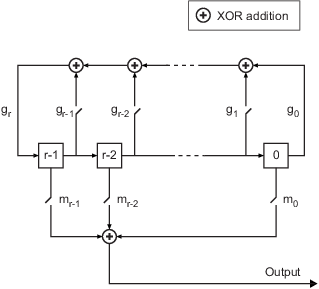
Initially I couldn’t find any source of information with a clear statement of what a primitive polynomial was, or how to find them. Standing on the Shoulders of Giants (Who Make Mistakes Once in a While)Ī couple of years after I first heard about LFSRs, sometime around 2004 or 2005, this primitive polynomial business was bugging me. Sometimes, though, a table isn’t good enough, or you want to double-check information from the table, or something like that. For example, the list of degree-5 polynomials contains 12 14 17 1B 1D 1E, and this is a different notation than I’ve been using, as it leaves out the unity term, so 12 hex = 10010 binary stands for the binary sequence 100101 = \( x^5 + x^2 + 1 \). Just be careful you interpret the listings correctly. Philip Koopman’s website - lots and lots of primitive polynomials up to degree 64 here.
Živković‘s A Table of Primitive Binary Polynomials (1994) - this lists trinomials, pentanomials, and septanomials.Īrash Partow’s website - this lists all primitive polynomials up to degree 8, and many primitive polynomials for higher degrees. Watson’s Primitive Polynomials (Mod 2) (1962) - this lists one primitive polynomial per degree, up to degree \( n=100 \), and also \( n=107 \) and \( n=127 \) thrown in for good measure. If you’re using a root-finding or maximum-finding algorithm, chances are it’s based on his research. This may not mean anything to you, but he’s one of the gurus of numerical analysis.

#Lfsr polynomial full
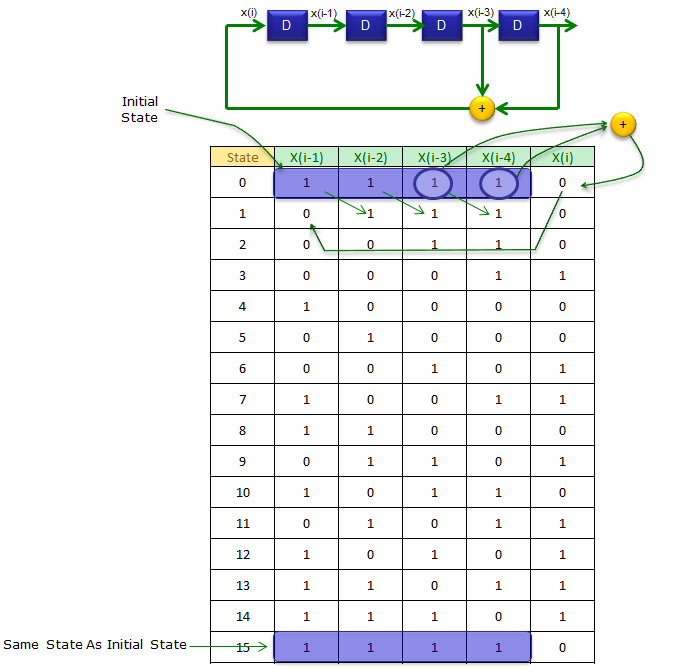
This is a result of Swan’s Theorem, which could be named the Curse-of-the-Octet Theorem, since you can’t use trinomials for any LFSRs which make full use of 8-bit-bytes for state storage. There are no irreducible or primitive trinomials of degrees that are multiples of 8.One of the things we discovered was that the polynomial \( x^ + 1 \) are primitive. Last time we figured out how to reverse-engineer parameters of an unknown CRC computation by providing sample inputs and analyzing the corresponding outputs.


 0 kommentar(er)
0 kommentar(er)
